位置




位置（いち、英語: position）とは、物体が空間の中のどこにあるかを表す量である。


原点 O から物体の位置 P へのベクトル（位置ベクトル (position vector)）で表される。通常は x, r, s で表され、O から P までの各軸に沿った直線距離に対応する[1]。


r=OP→{displaystyle mathbf {r} ={overrightarrow {OP}}}{displaystyle mathbf {r} ={overrightarrow {OP}}}

「位置ベクトル」という用語は、主に微分幾何学、力学、時にはベクトル解析の分野で使用される。


2次元または3次元空間で使用されることが多いが、任意の次元数のユークリッド空間に容易に一般化することができる[2]。




目次






  • 1 定義


    • 1.1 3次元


    • 1.2 n 次元




  • 2 応用


    • 2.1 微分幾何学


    • 2.2 力学




  • 3 位置の派生


  • 4 変位ベクトルとの関係


  • 5 関連項目


  • 6 脚注


  • 7 参考文献





定義



3次元




3次元の空間曲線。位置ベクトル r はスカラー量 t によってパラメータ化される。r = a では、赤い線は曲線の接線であり、青い面は曲線の法線である。


3次元では、任意の3次元座標とそれに対応する基底ベクトルを使用して、空間内の点の位置を定義することができる。位置の座標の表し方を座標系という。よく使われるのは直交座標系であり、ほかに球面座標系や円柱座標系が使用されることもある。


r(t)≡r(x,y,z)≡x(t)e^x+y(t)e^y+z(t)e^z≡r(r,θ,ϕ)≡r(t)e^r(θ(t),ϕ(t))≡r(r,θ,z)≡r(t)e^r(θ(t))+z(t)e^z⋯{displaystyle {begin{aligned}mathbf {r} (t)&equiv mathbf {r} left(x,y,zright)equiv x(t)mathbf {hat {e}} _{x}+y(t)mathbf {hat {e}} _{y}+z(t)mathbf {hat {e}} _{z}\&equiv mathbf {r} left(r,theta ,phi right)equiv r(t)mathbf {hat {e}} _{r}(theta (t),phi (t))\&equiv mathbf {r} left(r,theta ,zright)equiv r(t)mathbf {hat {e}} _{r}(theta (t))+z(t)mathbf {hat {e}} _{z}\&,!cdots \end{aligned}}}{displaystyle {begin{aligned}mathbf {r} (t)&equiv mathbf {r} left(x,y,zright)equiv x(t)mathbf {hat {e}} _{x}+y(t)mathbf {hat {e}} _{y}+z(t)mathbf {hat {e}} _{z}\&equiv mathbf {r} left(r,theta ,phi right)equiv r(t)mathbf {hat {e}} _{r}(theta (t),phi (t))\&equiv mathbf {r} left(r,theta ,zright)equiv r(t)mathbf {hat {e}} _{r}(theta (t))+z(t)mathbf {hat {e}} _{z}\&,!cdots \end{aligned}}}

ここで t は媒介変数である。


これらの異なる座標および対応する基底ベクトルは、同じ位置ベクトルを表す。より一般化した曲線座標（英語版）を代わりに使用することができ、連続体力学や一般相対性理論で使われる（後者の場合、追加の時間座標を必要とする）。



n 次元


線形代数では、n 次元の位置ベクトルの抽象化が可能である。位置ベクトルは、基底ベクトルの線形結合として表すことができる[3][4]。


r=∑i=1nxiei=x1e1+x2e2+⋯+xnen{displaystyle mathbf {r} =sum _{i=1}^{n}x_{i}mathbf {e} _{i}=x_{1}mathbf {e} _{1}+x_{2}mathbf {e} _{2}+dotsb +x_{n}mathbf {e} _{n}}{displaystyle mathbf {r} =sum _{i=1}^{n}x_{i}mathbf {e} _{i}=x_{1}mathbf {e} _{1}+x_{2}mathbf {e} _{2}+dotsb +x_{n}mathbf {e} _{n}}

全ての位置ベクトルの集合は、位置空間（要素が位置ベクトルであるベクトル空間）を形成する。空間内の別の位置ベクトルを得るために、位置を加算（ベクトル加算）し、長さを計測（スカラー乗算（英語版））することができる。それぞれの xi (i = 1, 2, …, n) は任意の値であり、値の集合は空間内の点を定義するので、「空間」の概念は直感的である。


位置空間の次元は n である（dim(R) = n とも示される）。基底ベクトル ei に対するベクトル r の座標は xi である。座標のベクトルは、座標ベクトルまたは n-タプル (x1, x2, …, xn)を形成する。


各座標 xi は、媒介変数 t でパラメータ化することができる。1つのパラメータ xi(t) は湾曲1次元経路を記述し、2つのパラメータ xi(t1, t2) は湾曲2次元表面を表し、3つのパラメータ xi(t1, t2, t3) は3次元空間を表す。


基底集合 B = {e1, e2, …, en} の線型包は、span(B) = R と表される位置空間 R に等しい。



応用



微分幾何学


詳細は「微分幾何学」を参照

位置ベクトルフィールドは、連続した微分可能な空間曲線を記述するために使用される。この場合、独立パラメータは時間でなくても、曲線の円弧長などでもかまわない。



力学


詳細は「ニュートン力学」、「解析力学」、および「運動方程式」を参照

任意の運動方程式において、位置ベクトル r(t) は、通常、最も時間が経過した後の量である。なぜなら、この関数は、ある時間 t における所与の座標系に対する粒子（点粒子）の運動を定義するからである。


位置に関して運動を定義するために、各座標は時間によってパラメータ化することができる。連続する各時間値は、座標によって与えられる連続する空間的位置の数列に対応するので、多くの連続する位置の連続限界は、粒子がトレースする経路である。


1次元の場合、位置は1つの成分しか持たないので、スカラー座標に効果的に縮退する。これは、例えば、x 方向または半径 r 方向のベクトルであり得る。同等の記法には、以下がある。


x≡x≡x(t),r≡r(t),s≡s(t)⋯{displaystyle mathbf {x} equiv xequiv x(t),quad requiv r(t),quad sequiv s(t)cdots ,!}{displaystyle mathbf {x} equiv xequiv x(t),quad requiv r(t),quad sequiv s(t)cdots ,!}


位置の派生




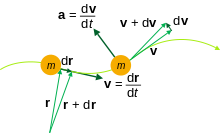
古典粒子の運動に関する量: 質量 m 、位置 r 、速度 v 、加速度 a


時間 t の関数である位置ベクトル r に対して、時間微分は t に関して計算することができる。これらの派生は、運動学、制御理論、工学および他の科学の研究において共通の有用性を有する。



速度

v=drdt{displaystyle mathbf {v} ={frac {mathrm {d} mathbf {r} }{mathrm {d} t}}}{displaystyle mathbf {v} ={frac {mathrm {d} mathbf {r} }{mathrm {d} t}}}


ここで、 dr は変位の微分小である。



加速度

a=dvdt=d2rdt2{displaystyle mathbf {a} ={frac {mathrm {d} mathbf {v} }{mathrm {d} t}}={frac {mathrm {d} ^{2}mathbf {r} }{mathrm {d} t^{2}}}}{displaystyle mathbf {a} ={frac {mathrm {d} mathbf {v} }{mathrm {d} t}}={frac {mathrm {d} ^{2}mathbf {r} }{mathrm {d} t^{2}}}}



躍度

j=dadt=d2vdt2=d3rdt3{displaystyle mathbf {j} ={frac {mathrm {d} mathbf {a} }{mathrm {d} t}}={frac {mathrm {d} ^{2}mathbf {v} }{mathrm {d} t^{2}}}={frac {mathrm {d} ^{3}mathbf {r} }{mathrm {d} t^{3}}}}{displaystyle mathbf {j} ={frac {mathrm {d} mathbf {a} }{mathrm {d} t}}={frac {mathrm {d} ^{2}mathbf {v} }{mathrm {d} t^{2}}}={frac {mathrm {d} ^{3}mathbf {r} }{mathrm {d} t^{3}}}}




位置の1階微分、2階微分、3階微分に対するこれらの名前は、基本的な運動学で一般的に使用される[5]。拡張によって、高次導関数は同様の方法で計算することができる。これらの高次導関数の研究は、元の変位関数の近似を改善することができる。 このようなより高次の項は、変位関数を無限の数列の和として正確に表現するために必要であり、工学および物理学におけるいくつかの解析技術を可能にする。



変位ベクトルとの関係


変位ベクトルは、与えられた距離にわたって所与の方向に空間点を一様に平行移動させる「動作」として定義することができる。従って、変位ベクトルの加算は、これらの変位動作の構成およびスカラー乗算を、距離の尺度として表現する。これを念頭に置いて、空間内の点の位置ベクトルを、ある点をその点に写像する変位ベクトルとして定義することができる。従って、位置ベクトルは空間の原点の選択に依存し、変位ベクトルは初期点の選択に依存することに留意されたい。



関連項目






ウィクショナリーに位置の項目があります。


  • アフィン空間


  • 6DoF (six degrees of freedom)

  • 線素（英語版）

  • パラメトリック曲面（英語版）

  • 位置エネルギー

  • 変位



脚注




  1. ^ H.D. Young, R.A. Freedman (2008). University Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 0-321-50130-6. 


  2. ^ Keller, F. J, Gettys, W. E. et al. (1993), p 28–29


  3. ^ Riley, K.F.; Hobson, M.P.; Bence, S.J. (2010). Mathematical methods for physics and engineering. Cambridge University Press. ISBN 978-0-521-86153-3. 


  4. ^ Lipschutz, S.; Lipson, M. (2009). Linear Algebra. McGraw Hill. ISBN 978-0-07-154352-1. 


  5. ^ Stewart, James (2001). “§2.8 - The Derivative As A Function”. Calculus (2nd ed.). Brooks/Cole. ISBN 0-534-37718-1. 



参考文献


  1. Keller, F. J, Gettys, W. E. et al. (1993). "Physics: Classical and modern" 2nd ed. McGraw Hill Publishing






  • 表

  • 話

  • 編

  • 歴


古典力学のSI単位















































































































線形・直線運動の量 角度・回転運動の量
次元 — L L2
 次元 — — —
T
時間: t
s
absement: A
m s（英語版）
 T
時間: t
s
—
距離: d, 位置: r, s, x, 変位
m
面積: A
m2
 —
角度: θ, 角変位（英語版）: θ
rad
 立体角: Ω
rad2, sr
T−1
周波数: f
s−1, Hz
速さ（速度の大きさ）: v, 速度: v
m s−1
動粘度: ν,
比角運動量（英語版）: h
m2 s−1
 T−1
周波数: f
s−1, Hz
 角速度（の大きさ）: ω, 角速度: ω
rad s−1
T−2
加速度: a
m s−2
 T−2
角加速度: α
rad s−2
T−3
躍度: j
m s−3
 T−3
角躍度: ζ
rad s−3
M
質量: m
kg
 M L2
慣性モーメント: I
kg m2
M T−1
運動量: p, 力積: J
kg m s−1, N s（英語版）
作用: 𝒮, actergy: ℵ
kg m2 s−1, J s（英語版）
 M L2 T−1
角運動量: L, 角力積: ΔL
kg m2 s−1
 作用: 𝒮, actergy: ℵ
kg m2 s−1, J s
M T−2
力: F, 重さ: Fg
kg m s−2, N
エネルギー: E, 仕事: W
kg m2 s−2, J
 M L2 T−2
トルク: τ, 力のモーメント: M
kg m2 s−2, N m
 エネルギー: E, 仕事: W
kg m2 s−2, J
M T−3
yank: Y
kg m s−3, N s−1
仕事率: P
kg m2 s−3, W
 M L2 T−3
rotatum: P
kg m2 s−3, N m s−1
 仕事率: P
kg m2 s−3, W




-

Popular posts from this blog

How to make a Squid Proxy server?

Image
1 I want to set up squid proxy server for monitoring user activity in a network and Internet Web URL filtering for user. I also want to configure the user login, user log, user access group, and block unwanted web sites in my network. Please help me and guide me the full process to do this. server proxy squid share | improve this question edited Jul 31 '12 at 14:45 Jorge Castro 37.1k 107 422 617 asked Jul 31 '12 at 5:16 Goivind Tiwari Goivind Tiwari ...
Read more

Is this a new Fibonacci Identity?

Image
6 1 $begingroup$ I have found the following Fibonacci Identity (and proved it). If $F_n$ denotes the nth Fibonacci Number, we have the following identity begin{equation} F_{n-r+h}F_{n+k+g+1} - F_{n-r+g}F_{n+k+h+1} = (-1)^{n+r+h+1} F_{g-h}F_{k+r+1} end{equation} where $F_1 = F_2 = 1$ , $r leq n$ , $h leq g$ , and $n, g, k in mathbb{N}$ . It is not too hard to show that this identity subsumes Cassini's Identity, Catalan's Identity, Vajda's Idenity, and d'Ocagne's identity to name a few. I have done a pretty thorough literature review, and I have not found anything like this, but I am still wondering if anyone has seen this identity before? I found this by accident after noticing some patterns in some analysis work I was doing, so if this is already known I would be curious to see w...
Read more

19世紀

Image
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。 （ 2012年3月 ） 千年紀: 2千年紀 世紀: 18世紀 - 19世紀 - 20世紀 十年紀: 1800年代 1810年代 1820年代 1830年代 1840年代 1850年代 1860年代 1870年代 1880年代 1890年代 19世紀に君臨した大英帝国。 19世紀 （じゅうきゅうせいき）は、西暦1801年から西暦1900年までの100年間を指す世紀。 目次 1 19世紀の歴史 1.1 国民国家の成立 1.2 帝国主義の興隆 1.3 列強の植民地争奪戦 2 できごと 2.1 1800年代 2.2 1810年代 2.3 1820年代 2.4 1830年代 2.5 1840年代 2.6 1850年代 2.7 1860年代 2.8 1870年代 2.9 1880年代 2.10 1890年代 2.11 1900年代 3 文化 3.1 文学 3.2 音楽 3.3 思想 3.4 科学 3.5 技術 4 人物 4.1 ヨーロッパ 4.1.1 政治家・王族 4.1.1.1 フランス 4.1.1.2 オーストリア＝ハンガリー 4.1.1.3 ロシア 4.1.1.4 イギリス 4.1.1.5 ドイツ（プロイセンほかドイツ領邦を含む） 4.1.1.6 北欧 4.1.1.7 イタリア 4.1.1.8 スペイン 4.1.1.9 ベルギー 4.1.1.10 ギリシア 4.1.2 軍人 4.1.3 実業家 4.1.4 科学と技術 4.1.5 思想と哲学・人文諸学 4.1.6 宗教 4.1.7 文学 4.1.8 美術 4.1.9 音楽 4.1.10 社会事業家 4.1.11 探検家・旅行家 4.1.12 料...
Read more