Are rainbows three dimensional? If so, what determines their depth? [duplicate]
$begingroup$
This question already has an answer here:
How deep is a rainbow?
2 answers
I am wondering whether rainbows are three dimensional, and if so, what determine their depth? How to calculate the depth of a rainbow, given its radius?
From what I understand, all rainbows are circular and their radius are determined by the distance between the observer and the water drops. How can one determine the depth based on this information, assuming the depth is non zero?
Edit: As stated in a comment by Solomon Slow, a rainbow is not really an object. My question still applies, the rays of light that make us see a rainbow are coming from droplets. What is the depth extension of these (real) droplets?
optics everyday-life reflection refraction atmospheric-science
asked 11 hours ago
t t t tt t t t
2,33831138
$endgroup$
marked as duplicate by Dan Yand, Buzz, David Z♦ 1 hour ago
This question has been asked before and already has an answer. If those answers do not fully address your question, please ask a new question.
add a comment |
$begingroup$
This question already has an answer here:
How deep is a rainbow?
2 answers
I am wondering whether rainbows are three dimensional, and if so, what determine their depth? How to calculate the depth of a rainbow, given its radius?
From what I understand, all rainbows are circular and their radius are determined by the distance between the observer and the water drops. How can one determine the depth based on this information, assuming the depth is non zero?
Edit: As stated in a comment by Solomon Slow, a rainbow is not really an object. My question still applies, the rays of light that make us see a rainbow are coming from droplets. What is the depth extension of these (real) droplets?
optics everyday-life reflection refraction atmospheric-science
asked 11 hours ago
t t t tt t t t
2,33831138
$endgroup$
marked as duplicate by Dan Yand, Buzz, David Z♦ 1 hour ago
This question has been asked before and already has an answer. If those answers do not fully address your question, please ask a new question.
1
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
1
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago
add a comment |
$begingroup$
This question already has an answer here:
How deep is a rainbow?
2 answers
I am wondering whether rainbows are three dimensional, and if so, what determine their depth? How to calculate the depth of a rainbow, given its radius?
From what I understand, all rainbows are circular and their radius are determined by the distance between the observer and the water drops. How can one determine the depth based on this information, assuming the depth is non zero?
Edit: As stated in a comment by Solomon Slow, a rainbow is not really an object. My question still applies, the rays of light that make us see a rainbow are coming from droplets. What is the depth extension of these (real) droplets?
optics everyday-life reflection refraction atmospheric-science
asked 11 hours ago
t t t tt t t t
2,33831138
$endgroup$
This question already has an answer here:
How deep is a rainbow?
2 answers
I am wondering whether rainbows are three dimensional, and if so, what determine their depth? How to calculate the depth of a rainbow, given its radius?
From what I understand, all rainbows are circular and their radius are determined by the distance between the observer and the water drops. How can one determine the depth based on this information, assuming the depth is non zero?
Edit: As stated in a comment by Solomon Slow, a rainbow is not really an object. My question still applies, the rays of light that make us see a rainbow are coming from droplets. What is the depth extension of these (real) droplets?
This question already has an answer here:
How deep is a rainbow?
2 answers
optics everyday-life reflection refraction atmospheric-science
optics everyday-life reflection refraction atmospheric-science
asked 11 hours ago
t t t tt t t t
2,33831138
asked 11 hours ago
t t t tt t t t
2,33831138
edited 10 hours ago
t t t t
asked 11 hours ago
t t t tt t t t
2,33831138
asked 11 hours ago
t t t tt t t t
2,33831138
asked 11 hours ago
t t t tt t t t
2,33831138
2,33831138
marked as duplicate by Dan Yand, Buzz, David Z♦ 1 hour ago
This question has been asked before and already has an answer. If those answers do not fully address your question, please ask a new question.
marked as duplicate by Dan Yand, Buzz, David Z♦ 1 hour ago
This question has been asked before and already has an answer. If those answers do not fully address your question, please ask a new question.
1
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
1
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago
add a comment |
1
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
1
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago
1
1
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
1
1
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago
add a comment |
3 Answers
3
active
oldest
votes
$begingroup$
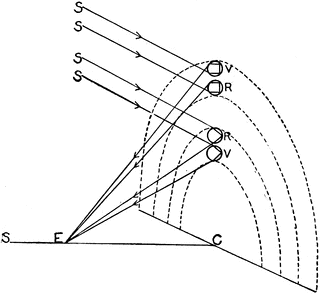
A rainbow doesn't strictly have a radius.
First: the obvious. A rainbow isn't a 'circle' but an annulus. The thickness comes from the range of frequencies (colors). However, if we restrict ourselves to one frequency, it's a circle.
No matter where you stand, the rainbow will appear as a circle centered around the antisolar point with an angle of $theta_{rm{crit}}approx 42^o$ (note, the image above shows 2 different angles - this is a double rainbow. You can ignore the outer rainbow.). If the rainbow was a definite distance $d$ from you, it would have a definite radius $r=d tan(theta_{rm{crit}})$. But it isn't!
The light which reaches your eye comes from any droplet of water located on a cone that has yourself as the vertex, the direction of sunlight as an axis and an angle of $theta_{rm{crit}}$. If the rain was confined to a thin sheet perpendicular to the sunlight (an obviously artificial configuration), only then would it's intersection with the cone be a definite circle with a definite radius.
As for determining thickness: roughly speaking a fainter rainbow should correspond to less thickness (fewer droplets contributing to the cone of light).
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
|
show 3 more comments
$begingroup$
In theory, if conditions are right, a rainbow can have a depth of several kilometres. But for this you would need the rainclouds to have just the right structure so that enough sunlight could get to the rain that they were producing, and then back to your eye. They would need to form a kind of enormous funnel. So that's not very likely. Also, the back of such a rainbow would contribute little to the spectacle, because the intervening rain would block out most of the reflected light.
In general, I would expect a decent rainbow to be of the order of hundreds of metres deep. This is not based on any scientific measurements, just on an understanding of the geometry involved.
answered 8 hours ago
TonyKTonyK
26316
$endgroup$
add a comment |
$begingroup$
No.
Rainbows aren't objects, so they don't have dimensions in the naïve sense.
Yes.
Rainbows are visible because droplets of water reflect and refract the sunlight into your eyes. The colors are refracted at slightly different angles, approximately at 42°. All droplets that are on a ray originating in your eye will refract the same color into your eye and depending on the current state of the atmosphere, there may be more or less droplets and they will probably be located in a certain volume that could be considered "the rainbow".
answered 8 hours ago
JasperJasper
8971516
$endgroup$
add a comment |
3 Answers
3
active
oldest
votes
3 Answers
3
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
A rainbow doesn't strictly have a radius.
First: the obvious. A rainbow isn't a 'circle' but an annulus. The thickness comes from the range of frequencies (colors). However, if we restrict ourselves to one frequency, it's a circle.
No matter where you stand, the rainbow will appear as a circle centered around the antisolar point with an angle of $theta_{rm{crit}}approx 42^o$ (note, the image above shows 2 different angles - this is a double rainbow. You can ignore the outer rainbow.). If the rainbow was a definite distance $d$ from you, it would have a definite radius $r=d tan(theta_{rm{crit}})$. But it isn't!
The light which reaches your eye comes from any droplet of water located on a cone that has yourself as the vertex, the direction of sunlight as an axis and an angle of $theta_{rm{crit}}$. If the rain was confined to a thin sheet perpendicular to the sunlight (an obviously artificial configuration), only then would it's intersection with the cone be a definite circle with a definite radius.
As for determining thickness: roughly speaking a fainter rainbow should correspond to less thickness (fewer droplets contributing to the cone of light).
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
|
show 3 more comments
$begingroup$
A rainbow doesn't strictly have a radius.
First: the obvious. A rainbow isn't a 'circle' but an annulus. The thickness comes from the range of frequencies (colors). However, if we restrict ourselves to one frequency, it's a circle.
No matter where you stand, the rainbow will appear as a circle centered around the antisolar point with an angle of $theta_{rm{crit}}approx 42^o$ (note, the image above shows 2 different angles - this is a double rainbow. You can ignore the outer rainbow.). If the rainbow was a definite distance $d$ from you, it would have a definite radius $r=d tan(theta_{rm{crit}})$. But it isn't!
The light which reaches your eye comes from any droplet of water located on a cone that has yourself as the vertex, the direction of sunlight as an axis and an angle of $theta_{rm{crit}}$. If the rain was confined to a thin sheet perpendicular to the sunlight (an obviously artificial configuration), only then would it's intersection with the cone be a definite circle with a definite radius.
As for determining thickness: roughly speaking a fainter rainbow should correspond to less thickness (fewer droplets contributing to the cone of light).
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
|
show 3 more comments
$begingroup$
A rainbow doesn't strictly have a radius.
First: the obvious. A rainbow isn't a 'circle' but an annulus. The thickness comes from the range of frequencies (colors). However, if we restrict ourselves to one frequency, it's a circle.
No matter where you stand, the rainbow will appear as a circle centered around the antisolar point with an angle of $theta_{rm{crit}}approx 42^o$ (note, the image above shows 2 different angles - this is a double rainbow. You can ignore the outer rainbow.). If the rainbow was a definite distance $d$ from you, it would have a definite radius $r=d tan(theta_{rm{crit}})$. But it isn't!
The light which reaches your eye comes from any droplet of water located on a cone that has yourself as the vertex, the direction of sunlight as an axis and an angle of $theta_{rm{crit}}$. If the rain was confined to a thin sheet perpendicular to the sunlight (an obviously artificial configuration), only then would it's intersection with the cone be a definite circle with a definite radius.
As for determining thickness: roughly speaking a fainter rainbow should correspond to less thickness (fewer droplets contributing to the cone of light).
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
$endgroup$
A rainbow doesn't strictly have a radius.
First: the obvious. A rainbow isn't a 'circle' but an annulus. The thickness comes from the range of frequencies (colors). However, if we restrict ourselves to one frequency, it's a circle.
No matter where you stand, the rainbow will appear as a circle centered around the antisolar point with an angle of $theta_{rm{crit}}approx 42^o$ (note, the image above shows 2 different angles - this is a double rainbow. You can ignore the outer rainbow.). If the rainbow was a definite distance $d$ from you, it would have a definite radius $r=d tan(theta_{rm{crit}})$. But it isn't!
The light which reaches your eye comes from any droplet of water located on a cone that has yourself as the vertex, the direction of sunlight as an axis and an angle of $theta_{rm{crit}}$. If the rain was confined to a thin sheet perpendicular to the sunlight (an obviously artificial configuration), only then would it's intersection with the cone be a definite circle with a definite radius.
As for determining thickness: roughly speaking a fainter rainbow should correspond to less thickness (fewer droplets contributing to the cone of light).
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
edited 10 hours ago
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
answered 10 hours ago
Tal SheafferTal Sheaffer
1724
1724
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
New contributor
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
Tal Sheaffer is a new contributor to this site. Take care in asking for clarification, commenting, and answering.
Check out our Code of Conduct.
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
|
show 3 more comments
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
2
2
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
I already know all of that, but your sketch is incomplete and does not deal with my question. In your sketch the rainbow is drew on a 2d surface. So your answer basically claims it's as if the light came out of a 2d object. Is that really so?
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
$begingroup$
And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away).
$endgroup$
– t t t t
10 hours ago
2
2
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
> "And by the way, it certainly has a radius. In your sketch, the CV segment (or CR, it makes almost no difference in a real situation where the rainbow is "far away)." That's because the sketch is only considering a thin sheet of rain. You can think a 'typical' rain as many thin sheets pressed together.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
Exactly and this is what I want to know. Say the vertical sheets do extend a lot in front/on the back. The rainbow will be formed by only a part of these sheets, not all, I suppose. I want to know how to compute that distance mathematically, given the distance between the observer and the drops.
$endgroup$
– t t t t
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
$begingroup$
I'm not sure I understand. Are you trying to build a picture of where in space the droplets are? As mentioned in the answer, the intensity of the light from the rainbow at a particular angle (azimuthal, not $theta$ which is constant) should roughly correspond to how many droplets lie on that line, so that gives you a very rough way to estimate the thickness. Other then that, I don't think there's anything you could do.
$endgroup$
– Tal Sheaffer
10 hours ago
|
show 3 more comments
$begingroup$
In theory, if conditions are right, a rainbow can have a depth of several kilometres. But for this you would need the rainclouds to have just the right structure so that enough sunlight could get to the rain that they were producing, and then back to your eye. They would need to form a kind of enormous funnel. So that's not very likely. Also, the back of such a rainbow would contribute little to the spectacle, because the intervening rain would block out most of the reflected light.
In general, I would expect a decent rainbow to be of the order of hundreds of metres deep. This is not based on any scientific measurements, just on an understanding of the geometry involved.
answered 8 hours ago
TonyKTonyK
26316
$endgroup$
add a comment |
$begingroup$
In theory, if conditions are right, a rainbow can have a depth of several kilometres. But for this you would need the rainclouds to have just the right structure so that enough sunlight could get to the rain that they were producing, and then back to your eye. They would need to form a kind of enormous funnel. So that's not very likely. Also, the back of such a rainbow would contribute little to the spectacle, because the intervening rain would block out most of the reflected light.
In general, I would expect a decent rainbow to be of the order of hundreds of metres deep. This is not based on any scientific measurements, just on an understanding of the geometry involved.
answered 8 hours ago
TonyKTonyK
26316
$endgroup$
add a comment |
$begingroup$
In theory, if conditions are right, a rainbow can have a depth of several kilometres. But for this you would need the rainclouds to have just the right structure so that enough sunlight could get to the rain that they were producing, and then back to your eye. They would need to form a kind of enormous funnel. So that's not very likely. Also, the back of such a rainbow would contribute little to the spectacle, because the intervening rain would block out most of the reflected light.
In general, I would expect a decent rainbow to be of the order of hundreds of metres deep. This is not based on any scientific measurements, just on an understanding of the geometry involved.
answered 8 hours ago
TonyKTonyK
26316
$endgroup$
In theory, if conditions are right, a rainbow can have a depth of several kilometres. But for this you would need the rainclouds to have just the right structure so that enough sunlight could get to the rain that they were producing, and then back to your eye. They would need to form a kind of enormous funnel. So that's not very likely. Also, the back of such a rainbow would contribute little to the spectacle, because the intervening rain would block out most of the reflected light.
In general, I would expect a decent rainbow to be of the order of hundreds of metres deep. This is not based on any scientific measurements, just on an understanding of the geometry involved.
answered 8 hours ago
TonyKTonyK
26316
answered 8 hours ago
TonyKTonyK
26316
answered 8 hours ago
TonyKTonyK
26316
answered 8 hours ago
TonyKTonyK
26316
26316
add a comment |
add a comment |
$begingroup$
No.
Rainbows aren't objects, so they don't have dimensions in the naïve sense.
Yes.
Rainbows are visible because droplets of water reflect and refract the sunlight into your eyes. The colors are refracted at slightly different angles, approximately at 42°. All droplets that are on a ray originating in your eye will refract the same color into your eye and depending on the current state of the atmosphere, there may be more or less droplets and they will probably be located in a certain volume that could be considered "the rainbow".
answered 8 hours ago
JasperJasper
8971516
$endgroup$
add a comment |
$begingroup$
No.
Rainbows aren't objects, so they don't have dimensions in the naïve sense.
Yes.
Rainbows are visible because droplets of water reflect and refract the sunlight into your eyes. The colors are refracted at slightly different angles, approximately at 42°. All droplets that are on a ray originating in your eye will refract the same color into your eye and depending on the current state of the atmosphere, there may be more or less droplets and they will probably be located in a certain volume that could be considered "the rainbow".
answered 8 hours ago
JasperJasper
8971516
$endgroup$
add a comment |
$begingroup$
No.
Rainbows aren't objects, so they don't have dimensions in the naïve sense.
Yes.
Rainbows are visible because droplets of water reflect and refract the sunlight into your eyes. The colors are refracted at slightly different angles, approximately at 42°. All droplets that are on a ray originating in your eye will refract the same color into your eye and depending on the current state of the atmosphere, there may be more or less droplets and they will probably be located in a certain volume that could be considered "the rainbow".
answered 8 hours ago
JasperJasper
8971516
$endgroup$
No.
Rainbows aren't objects, so they don't have dimensions in the naïve sense.
Yes.
Rainbows are visible because droplets of water reflect and refract the sunlight into your eyes. The colors are refracted at slightly different angles, approximately at 42°. All droplets that are on a ray originating in your eye will refract the same color into your eye and depending on the current state of the atmosphere, there may be more or less droplets and they will probably be located in a certain volume that could be considered "the rainbow".
answered 8 hours ago
JasperJasper
8971516
answered 8 hours ago
JasperJasper
8971516
answered 8 hours ago
JasperJasper
8971516
answered 8 hours ago
JasperJasper
8971516
8971516
add a comment |
add a comment |
1
$begingroup$
@tttt, it is probably more relevant to ask about how many water droplets are at the appropriate angle to produce a rainbow. Those water droplets don't have a definite depth, but the DO have a definite angle.
$endgroup$
– David White
9 hours ago
$begingroup$
@DavidWhite Yeah, that's the solution to my question. If the could extends infinitely, the depth would be infinite. I did not realize this! I thought there was a finite depth that would depend on the distance between the observer and the drops.
$endgroup$
– t t t t
9 hours ago
1
$begingroup$
Duplicate How deep is a rainbow and links therein.
$endgroup$
– Farcher
9 hours ago