Ytdyklly

斜方切頂立方八面体
種別	半正多面体、ゾーン多面体
面数	26
面形状	正方形: 12 正六角形: 8 正八角形: 6
辺数	72
頂点数	48
頂点形状	4, 6, 8（正方形1枚と正六角形1枚、正八角形1枚が集まる）
シュレーフリ記号	tr{4, 3}
ワイソフ記号	2 3 4 |
対称群	Oh
双対多面体	六方八面体
特性	凸集合
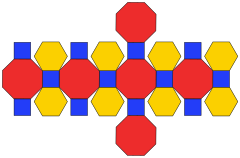展開図
テンプレートを表示

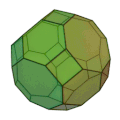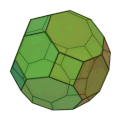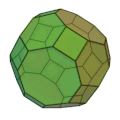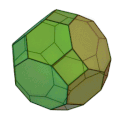
斜方切頂立方八面体（しゃほうせっちょうりっぽうはちめんたい、英: rhombitruncated cuboctahedron）、または大菱形立方八面体^[1]（だいりょうけいりっぽうはちめんたい、英: great rhombicuboctahedron）、切頂立方八面体（せっちょうりっぽうはちめんたい、英: truncated cuboctahedron）、切頭立方八面体^[1]（せっとうりっぽうはちめんたい）、角切り立方八面体（かくぎりりっぽうはちめんたい）とは、半正多面体の一種で、立方八面体の各頂点を切り落としたような立体である。ただし、正確に立方八面体の各頂点を切り落とした形にはなっていない。

性質

赤い面は正六面体由来、青い面は正八面体由来、黄色い面は菱形十二面体由来

• 
  表面積: 一辺をa{displaystyle a}とすると S=(24+122+123)a2{displaystyle S=(24+12{sqrt {2}}+12{sqrt {3}})a^{2}}
  


• 
  体積: 一辺をa{displaystyle a}とすると V=(22+142)a3{displaystyle V=(22+14{sqrt {2}})a^{3}}
  


• 外接球半径: 一辺を2とすると13+62{displaystyle {sqrt {13+6{sqrt {2}}}}}
  


• 
  ゾーン多面体の一種でもある。

この図形の不正確なものと頂点が共通となる立体

• 
  

  

  
  

  
  

  立方切頂立方八面体
  

  
  

  
  


• 
  

  

  
  

  
  

  大切頂立方八面体
  

  
  

  
  

近縁な立体

• 
  

  

  
  

  
  

  立方八面体
  （ベースの形）
  

  
  

  
  


• 
  

  

  
  

  
  

  斜方立方八面体
  （切り込みを深くする）
  

  
  

  
  


• 
  

  

  
  

  
  

  斜方切頂立方八面体と六方八面体による複合多面体
  

  
  

  
  

関連項目

• 斜方切頂二十・十二面体


• 
  一様大斜方立方八面体 - 英語名Great rhombicuboctahedronはこの意味も持つ。

出典

1. ^ ^abダウド・サットン（2005）『プラトンとアルキメデスの立体 - 三次元に浮かびあがる美の世界』（青木 薫訳）ランダムハウス講談社
   

外部リンク

• Weisstein, Eric W. "Great Rhombicuboctahedron". MathWorld（英語）. CS1 maint: Multiple names: authors list

表 話 編 歴 多面体 一様多面体 正多面体 正四面体 正六面体 正八面体 正十二面体 正二十面体 半正多面体 切頂四面体 切頂六面体 切頂八面体 切頂十二面体 切頂二十面体 立方八面体 二十・十二面体 斜方立方八面体 斜方二十・十二面体 斜方切頂立方八面体 斜方切頂二十・十二面体 変形立方体 変形十二面体 星型正多面体 小星型十二面体 大十二面体 大星型十二面体 大二十面体 その他 八面半八面体 四面半六面体 小立方立方八面体 大立方立方八面体 立方半八面体 立方切頂立方八面体 一様大斜方立方八面体 小斜方六面体 星型切頂六面体 大切頂立方八面体 大斜方六面体 小二重三角二十・十二面体 小二十・二十・十二面体 小変形二十・二十・十二面体 小十二・二十・十二面体 十二・十二面体 切頂大十二面体 斜方十二・十二面体 小斜方十二面体 変形十二・十二面体 二重三角十二・十二面体 大二重三角十二・二十・十二面体 小二重三角十二・二十・十二面体 二十・十二・十二面体 二十面切頂十二・十二面体 変形二十・十二・十二面体 大二重三角二十・十二面体 大二十・二十・十二面体 小二十面半十二面体 小十二・二十面体 小十二面半十二面体 大二十・十二面体 切頂大二十面体 斜方二十面体 大変形二十・十二面体 小星型切頂十二面体 切頂十二・十二面体 逆変形十二・十二面体 大十二・二十・十二面体 小十二面半二十面体 大十二・二十面体 大変形十二・二十・十二面体 大十二面半二十面体 大星型切頂十二面体 一様大斜方二十・十二面体 大切頂二十・十二面体 大逆変形二十・十二面体 大十二面半十二面体 大二十面半十二面体 小反屈変形二十・二十・十二面体 大斜方十二面体 大反屈変形二十・十二面体 大二重斜方二十・十二面体 カタランの立体 三方四面体 三方八面体 四方六面体 三方二十面体 五方十二面体 菱形十二面体 菱形三十面体 凧形二十四面体 凧形六十面体 六方八面体 六方二十面体 五角二十四面体 五角六十面体 ジョンソンの立体 正四角錐 正五角錐 正三角台塔 正四角台塔 正五角台塔 正五角丸塔 正三角錐柱 正四角錐柱 正五角錐柱 正四角錐反柱 正五角錐反柱 双三角錐 双五角錐 双三角錐柱 双四角錐柱 双五角錐柱 双四角錐反柱 正三角台塔柱 正四角台塔柱 正五角台塔柱 正五角丸塔柱 正三角台塔反柱 正四角台塔反柱 正五角台塔反柱 正五角丸塔反柱 異相双三角柱 同相双三角台塔 同相双四角台塔 異相双四角台塔 同相双五角台塔 異相双五角台塔 同相五角台塔丸塔 異相五角台塔丸塔 同相双五角丸塔 同相双三角台塔柱 異相双三角台塔柱 異相双四角台塔柱 同相双五角台塔柱 異相双五角台塔柱 同相五角台塔丸塔柱 異相五角台塔丸塔柱 同相双五角丸塔柱 異相双五角丸塔柱 双三角台塔反柱 双四角台塔反柱 双五角台塔反柱 五角台塔丸塔反柱 双五角丸塔反柱 側錐三角柱 二側錐三角柱 三側錐三角柱 側錐五角柱 二側錐五角柱 側錐六角柱 双側錐六角柱 二側錐六角柱 三側錐六角柱 側錐十二面体 双側錐十二面体 二側錐十二面体 三側錐十二面体 二側錐欠損二十面体 三側錐欠損二十面体 側錐三側錐欠損二十面体 側台塔切頂四面体 側台塔切頂立方体 双側台塔切頂立方体 側台塔切頂十二面体 双側台塔切頂十二面体 二側台塔切頂十二面体 三側台塔切頂十二面体 側台塔回転斜方二十・十二面体 双側台塔回転斜方二十・十二面体 二側台塔回転斜方二十・十二面体 三側台塔回転斜方二十・十二面体 側台塔欠損斜方二十・十二面体 双側台塔回転欠損斜方二十・十二面体 二側台塔回転欠損斜方二十・十二面体 二側台塔回転側台塔欠損斜方二十・十二面体 双側台塔欠損斜方二十・十二面体 二側台塔欠損斜方二十・十二面体 側台塔回転二側台塔欠損斜方二十・十二面体 三側台塔欠損斜方二十・十二面体 変形双五角錐 変形四角反柱 球形屋根 側錐球形屋根 長球形屋根 広底長球形屋根 五角錐球形屋根 双三日月双丸塔 三角広底球形屋根丸塔 ゾーン多面体 平行六面体 菱形十二面体第2種 菱形二十面体 菱形九十面体 長菱形十二面体 星型多面体 小三角六辺形二十面体 完全二十面体 星型八面体 ねじれ正多面体 四角六片四角孔ねじれ正多面体 六角四片四角孔ねじれ正多面体 六角六片三角孔ねじれ正多面体 面の数による分類 二面体 四面体 五面体 六面体 七面体 八面体 十面体 十二面体 十四面体 二十面体 二十四面体 三十面体 四十八面体 六十面体 百二十面体 その他 角錐 角柱 双角錐 反角柱 ねじれ双角錐 プリズマトイド（英語版） 擬大斜方立方八面体 大二重変形二重斜方十二面体 切稜立方体 穿孔多面体 ダ・ヴィンチの星 正四面体リング 凸多面体 凹多面体 双対多面体 複合多面体 平面充填形

この項目は、多面体に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています。