Ytdyklly

半正多面体 (はんせいためんたい、semi-regular polyhedron) またはアルキメデスの立体 (Archimedean solid) とは、凸な一様多面体のうち、正多面体以外のものである。また、対称性が低い (Dihedral) 角柱・反角柱・ミラーの立体も除く。全部で13種類ある。

一様多面体の条件は、全ての面が正多角形で、頂点形状が合同（頂点に集まる正多角形の種類と順序が同じ）なことである。正多面体（別名：プラトンの立体）は除外するので、半正多面体の面は2種類以上の正多角形で構成される。

準正多面体 (quasi-regular polyhedron) とは、このうち辺の近傍が合同なもので、立方八面体と二十・十二面体が当てはまる。日本では、半正多面体のことを準正多面体ということがあるが、誤りである^[1]。

一覧

多面体	構成面	辺	頂点	頂点形状	双対	図
切頂四面体	正三角形 4枚 正六角形 4枚	18	12	3,6,6	三方四面体
切頂六面体	正三角形 8枚 正八角形 6枚	36	24	3,8,8	三方八面体
切頂八面体	正方形 6枚 正六角形 8枚	36	24	4,6,6	四方六面体
切頂十二面体	正三角形 20枚 正十角形 12枚	90	60	3,10,10	三方二十面体
切頂二十面体 （サッカーボール型）	正五角形 12枚 正六角形 20枚	90	60	5,6,6	五方十二面体
立方八面体	正三角形 8枚 正方形 6枚	24	12	3,4,3,4	菱形十二面体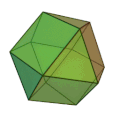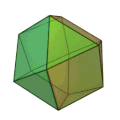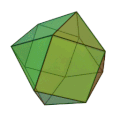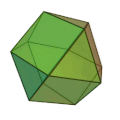
二十・十二面体	正三角形 20枚 正五角形 12枚	60	30	3,5,3,5	菱形三十面体
斜方立方八面体	正三角形 8枚 正方形 18枚	48	24	3,4,4,4	凧形二十四面体
斜方二十・十二面体	正三角形 20枚 正方形 30枚 正五角形 12枚	120	60	3,4,5,4	凧形六十面体
斜方切頂立方八面体	正方形 12枚 正六角形 8枚 正八角形 6枚	72	48	4,6,8	六方八面体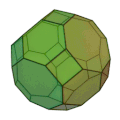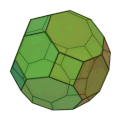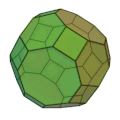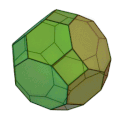
斜方切頂二十・十二面体	正方形 30枚 正六角形 20枚 正十角形 12枚	180	120	4,6,10	六方二十面体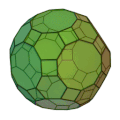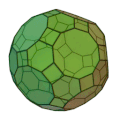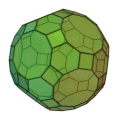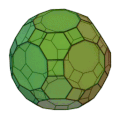
変形立方体 （鏡像あり）	正三角形 32枚 正方形 6枚	60	24	3,3,3,3,4	五角二十四面体
変形十二面体 （鏡像あり）	正三角形 80枚 正五角形 12枚	150	60	3,3,3,3,5	五角六十面体

半正多面体でない多面体

「面が正多角形で頂点形状が合同」という条件を満たすが、対称性が低いために半正多面体に含められない多面体に、ミラーの立体・アルキメデスの角柱・アルキメデスの反角柱がある。

ミラーの立体は、斜方立方八面体の上半分を45度ひねった多面体である。ただし、ミラーの立体を半正多面体に含め、キラルな変形立方体と変形十二面体の鏡像を区別し、半正多面体を16種類とする場合もある。

アルキメデスの正角柱とアルキメデスの反角柱を含めないのは、種類が無限にあることも理由である。アルキメデスの立体と言った場合は含むこともある。

正多面体からの作製

半正多面体を正多面体から作るときの方法は5種類ある。それは以下のとおりである。

切頂 n 面体

正 n 面体の頂点を切ったもの。切隅 n 面体、切頭 n 面体とも。拡張シュレーフリ記号は t{p, q}

n・m 面体（準正多面体）

正 n または m 面体の頂点を各辺の中点まで切ったもの。拡張シュレーフリ記号は {pq}{displaystyle {begin{Bmatrix}p\qend{Bmatrix}}}

斜方 n・m 面体

正 n または m 面体の各辺と頂点を削ったもの。小斜方 n・m 面体、菱形 n・m 面体とも。拡張シュレーフリ記号は r{pq}{displaystyle r{begin{Bmatrix}p\qend{Bmatrix}}}

斜方切頂 n・m 面体

n・m 面体の頂点を切ったもの。切頂 n・m 面体、大斜方 n・m 面体とも。拡張シュレーフリ記号は t{pq}{displaystyle t{begin{Bmatrix}p\qend{Bmatrix}}}

変形 n 面体

正 n 面体の各面をひねったもの。鏡像がある。捩れ n 面体とも。拡張シュレーフリ記号は s{pq}{displaystyle s{begin{Bmatrix}p\qend{Bmatrix}}}

双対

半正多面体の双対は、アルキメデス双対と呼ばれる。1種類の正多角形でない面からできており、頂点に集まる面の頂点角は等しい。

出典

1. 
   ^ 「誤訳」者自身による説明
   

表 話 編 歴 多面体 一様多面体 正多面体 正四面体 正六面体 正八面体 正十二面体 正二十面体 半正多面体 切頂四面体 切頂六面体 切頂八面体 切頂十二面体 切頂二十面体 立方八面体 二十・十二面体 斜方立方八面体 斜方二十・十二面体 斜方切頂立方八面体 斜方切頂二十・十二面体 変形立方体 変形十二面体 星型正多面体 小星型十二面体 大十二面体 大星型十二面体 大二十面体 その他 八面半八面体 四面半六面体 小立方立方八面体 大立方立方八面体 立方半八面体 立方切頂立方八面体 一様大斜方立方八面体 小斜方六面体 星型切頂六面体 大切頂立方八面体 大斜方六面体 小二重三角二十・十二面体 小二十・二十・十二面体 小変形二十・二十・十二面体 小十二・二十・十二面体 十二・十二面体 切頂大十二面体 斜方十二・十二面体 小斜方十二面体 変形十二・十二面体 二重三角十二・十二面体 大二重三角十二・二十・十二面体 小二重三角十二・二十・十二面体 二十・十二・十二面体 二十面切頂十二・十二面体 変形二十・十二・十二面体 大二重三角二十・十二面体 大二十・二十・十二面体 小二十面半十二面体 小十二・二十面体 小十二面半十二面体 大二十・十二面体 切頂大二十面体 斜方二十面体 大変形二十・十二面体 小星型切頂十二面体 切頂十二・十二面体 逆変形十二・十二面体 大十二・二十・十二面体 小十二面半二十面体 大十二・二十面体 大変形十二・二十・十二面体 大十二面半二十面体 大星型切頂十二面体 一様大斜方二十・十二面体 大切頂二十・十二面体 大逆変形二十・十二面体 大十二面半十二面体 大二十面半十二面体 小反屈変形二十・二十・十二面体 大斜方十二面体 大反屈変形二十・十二面体 大二重斜方二十・十二面体 カタランの立体 三方四面体 三方八面体 四方六面体 三方二十面体 五方十二面体 菱形十二面体 菱形三十面体 凧形二十四面体 凧形六十面体 六方八面体 六方二十面体 五角二十四面体 五角六十面体 ジョンソンの立体 正四角錐 正五角錐 正三角台塔 正四角台塔 正五角台塔 正五角丸塔 正三角錐柱 正四角錐柱 正五角錐柱 正四角錐反柱 正五角錐反柱 双三角錐 双五角錐 双三角錐柱 双四角錐柱 双五角錐柱 双四角錐反柱 正三角台塔柱 正四角台塔柱 正五角台塔柱 正五角丸塔柱 正三角台塔反柱 正四角台塔反柱 正五角台塔反柱 正五角丸塔反柱 異相双三角柱 同相双三角台塔 同相双四角台塔 異相双四角台塔 同相双五角台塔 異相双五角台塔 同相五角台塔丸塔 異相五角台塔丸塔 同相双五角丸塔 同相双三角台塔柱 異相双三角台塔柱 異相双四角台塔柱 同相双五角台塔柱 異相双五角台塔柱 同相五角台塔丸塔柱 異相五角台塔丸塔柱 同相双五角丸塔柱 異相双五角丸塔柱 双三角台塔反柱 双四角台塔反柱 双五角台塔反柱 五角台塔丸塔反柱 双五角丸塔反柱 側錐三角柱 二側錐三角柱 三側錐三角柱 側錐五角柱 二側錐五角柱 側錐六角柱 双側錐六角柱 二側錐六角柱 三側錐六角柱 側錐十二面体 双側錐十二面体 二側錐十二面体 三側錐十二面体 二側錐欠損二十面体 三側錐欠損二十面体 側錐三側錐欠損二十面体 側台塔切頂四面体 側台塔切頂立方体 双側台塔切頂立方体 側台塔切頂十二面体 双側台塔切頂十二面体 二側台塔切頂十二面体 三側台塔切頂十二面体 側台塔回転斜方二十・十二面体 双側台塔回転斜方二十・十二面体 二側台塔回転斜方二十・十二面体 三側台塔回転斜方二十・十二面体 側台塔欠損斜方二十・十二面体 双側台塔回転欠損斜方二十・十二面体 二側台塔回転欠損斜方二十・十二面体 二側台塔回転側台塔欠損斜方二十・十二面体 双側台塔欠損斜方二十・十二面体 二側台塔欠損斜方二十・十二面体 側台塔回転二側台塔欠損斜方二十・十二面体 三側台塔欠損斜方二十・十二面体 変形双五角錐 変形四角反柱 球形屋根 側錐球形屋根 長球形屋根 広底長球形屋根 五角錐球形屋根 双三日月双丸塔 三角広底球形屋根丸塔 ゾーン多面体 平行六面体 菱形十二面体第2種 菱形二十面体 菱形九十面体 長菱形十二面体 星型多面体 小三角六辺形二十面体 完全二十面体 星型八面体 ねじれ正多面体 四角六片四角孔ねじれ正多面体 六角四片四角孔ねじれ正多面体 六角六片三角孔ねじれ正多面体 面の数による分類 二面体 四面体 五面体 六面体 七面体 八面体 十面体 十二面体 十四面体 二十面体 二十四面体 三十面体 四十八面体 六十面体 百二十面体 その他 角錐 角柱 双角錐 反角柱 ねじれ双角錐 プリズマトイド（英語版） 擬大斜方立方八面体 大二重変形二重斜方十二面体 切稜立方体 穿孔多面体 ダ・ヴィンチの星 正四面体リング 凸多面体 凹多面体 双対多面体 複合多面体 平面充填形